
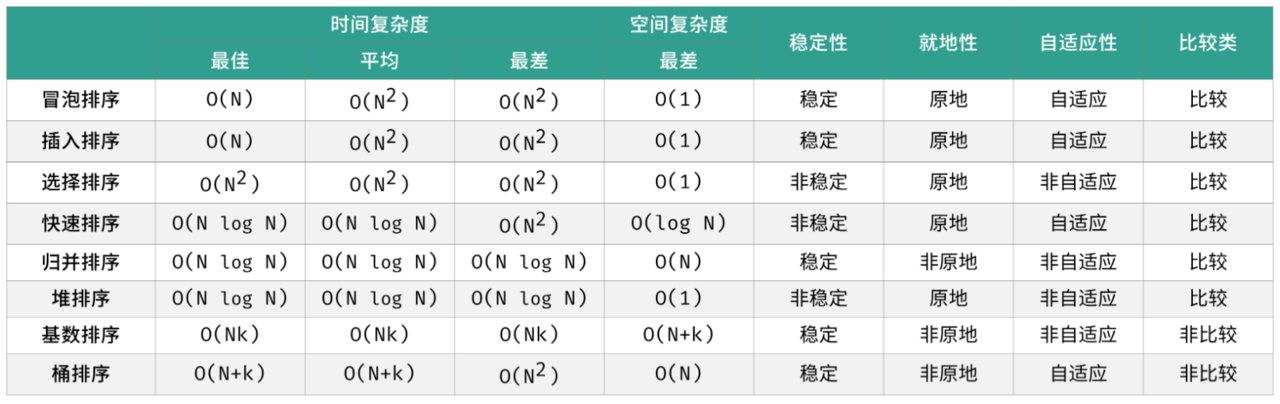
选取了最常见的八种排序算法:冒泡排序、插入排序、选择排序、快速排序、归并排序、堆排序、基数排序、桶排序,做一个整理和对比。
每个算法的细节不一一展开,直接上表,对比不同算法之间的时空复杂度及其特性。
public class BubbleSort {
void bubbleSort(int[] nums) {
int n = nums.length;
int tmp;
boolean flag;
for (int i = 0; i < n - 1; i++) {
flag = false;
for (int j = 0; j < n - i - 1; j++) {
if (nums[j] > nums[j + 1]) {
tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
flag = true;
}
}
if (!flag) {
break;
}
}
}
}
public class InsertionSort {
void insertionSort(int[] nums) {
int n = nums.length;
for (int i = 1; i < n; i++) {
int j = i;
while (j > 0) {
if (nums[j] < nums[j - 1]) {
int tmp = nums[j];
nums[j] = nums[j - 1];
nums[j - 1] = tmp;
j--;
} else {
break;
}
}
}
}
}
public class SelectionSort {
void selectionSort(int[] nums) {
int n = nums.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (nums[j] < nums[minIndex]) {
minIndex = j;
}
}
if (minIndex != i) {
int tmp = nums[minIndex];
nums[minIndex] = nums[i];
nums[i] = tmp;
}
}
}
}
public class QuickSort {
void quickSort(int[] nums, int l, int r) {
while (l < r) {
int i = partition(nums, l, r);
// Tail Call:仅递归至较短子数组,控制递归深度
if (i - l < r - i) {
quickSort(nums, l, i - 1);
l = i + 1;
} else {
quickSort(nums, i + 1, r);
r = i - 1;
}
}
}
int partition(int[] nums, int l, int r) {
// 随机基准数:闭区间[l, r]随机选取任意索引,并与nums[l]交换,防止最差时间复杂度
int ra = (int) (l + Math.random() * (r - l + 1));
swap(nums, l, ra);
// 基准数:nums[l]
int i = l, j = r;
while (i < j) {
while (i < j && nums[j] >= nums[l]) {
j--;
}
while (i < j && nums[i] <= nums[l]) {
i++;
}
swap(nums, i, j);
}
swap(nums, i, l);
return i;
}
void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
public class MergeSort {
void mergeSort(int[] nums, int l, int r) {
if (l >= r) {
return;
}
int m = (l + r) / 2;
mergeSort(nums, l, m);
mergeSort(nums, m + 1, r);
// 暂存需要合并区间的元素
int[] tmp = new int[r - l + 1];
for (int k = l; k <= r; k++) {
tmp[k - l] = nums[k];
}
// 左右指针首元素
int i = 0, j = m - l + 1;
// 遍历合并左右数组
for (int k = l; k <= r; k++) {
if (i == m - l + 1) {
nums[k] = tmp[j++];
} else if (j == r - l + 1 || tmp[i] <= tmp[j]) {
nums[k] = tmp[i++];
} else {
nums[k] = tmp[j++];
}
}
}
}
public class HeapSort {
void heapSort(int[] nums) {
int n = nums.length;
// 构建大顶堆
buildMaxHeap(nums, n);
for (int i = n - 1; i > 0; i--) {
// 将大顶堆堆首元素与堆尾元素交换(堆选择排序将最大值放大数组尾部)
swap(nums, 0, i);
n--;
// 维护交换后的树满足大顶堆性质
heapify(nums, 0, n);
}
}
/**
* 构建大顶堆
* 从最后一个非叶子节点(len / 2 - 1)开始,若父节点小于子节点则交换位置
* 依次从右至左,从下至上
*/
void buildMaxHeap(int[] nums, int len) {
for (int i = len / 2 - 1; i >= 0; i--) {
heapify(nums, i, len);
}
}
/**
* 维护大顶堆性质
* 左右叶子节点小于父节点
*/
void heapify(int[] nums, int i, int len) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left < len && nums[left] > nums[largest]) {
largest = left;
}
if (right < len && nums[right] > nums[largest]) {
largest = right;
}
if (largest != i) {
swap(nums, i, largest);
// 以交换节点作为父节点递归维护子树的大顶堆性质
heapify(nums, largest, len);
}
}
void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
public class RadixSort {
void radixSort(int[] nums) {
int maxDigit = getMaxDigit(nums);
int div = 1;
int[] count = new int[10];
int[] result = new int[nums.length];
for (int i = 0; i < maxDigit; i++) {
for (int num : nums) {
int pos = num / div % 10;
count[pos]++;
}
for (int j = 1; j < count.length; j++) {
count[j] = count[j] + count[j - 1];
}
for (int j = nums.length - 1; j >= 0; j--) {
int pos = nums[j] / div % 10;
result[--count[pos]] = nums[j];
}
System.arraycopy(result, 0, nums, 0, nums.length);
Arrays.fill(count, 0);
div *= 10;
}
}
/**
* 获取最高位位数
*/
int getMaxDigit(int[] nums) {
int maxValue = nums[0];
for (int value : nums) {
if (value > maxValue) {
maxValue = value;
}
}
if (maxValue == 0) {
return 1;
}
int length = 0;
for (long tmp = maxValue; tmp != 0; tmp /= 10) {
length++;
}
return length;
}
}
public class BucketSort {
int BUCKET_SIZE = 10;
void bucketSort(int[] nums) {
int minValue = nums[0];
int maxValue = nums[0];
for (int value : nums) {
if (value < minValue) {
minValue = value;
} else if (value > maxValue) {
maxValue = value;
}
}
int bucketCount = (maxValue - minValue) / BUCKET_SIZE + 1;
int[][] buckets = new int[bucketCount][0];
// 利用映射函数分配数据到桶中
for (int num : nums) {
int index = (num - minValue) / BUCKET_SIZE;
buckets[index] = arrayAppend(buckets[index], num);
}
int arrIndex = 0;
for (int[] bucket : buckets) {
if (bucket.length <= 0) {
continue;
}
// 对每个桶进行排序,桶内自主排序使用快速排序算法
QuickSort s = new QuickSort();
s.quickSort(bucket, 0, bucket.length - 1);
for (int value : bucket) {
nums[arrIndex++] = value;
}
}
}
/**
* 数组自动扩容
*/
int[] arrayAppend(int[] nums, int value) {
nums = Arrays.copyOf(nums, nums.length + 1);
nums[nums.length - 1] = value;
return nums;
}
}
对数组长度分别为 10000、100000、300000 的数组进行测试,不同的排序算法的耗时情况如下,本来想测到100W的数据量,但无耐冒泡实在太慢,不过30W的数据量已经很有区分度了。
测试结果仅具有参考价值,因为其会算测试环境性能及其他条件所影响,且桶排序本身不具备可比性,其性能特点是根据其内部的排序算法所决定,并且还受分配的桶的个数所影响。
public class Testing {
static int NUMS_LENGTH = 300000; // 数组长度
static int MIN_VALUE = 1; // 随机数最小值
static int MAX_VALUE = 99999999; // 随机数最大值
public static int[] getRandomNums() {
int[] nums = new int[NUMS_LENGTH];
Random random = new Random();
for (int i = 0; i < NUMS_LENGTH; i++) {
nums[i] = random.nextInt(MAX_VALUE) + MIN_VALUE;
}
return nums;
}
public static void main(String[] args) {
BubbleSort bubbleSort = new BubbleSort();
BucketSort bucketSort = new BucketSort();
HeapSort heapSort = new HeapSort();
InsertionSort insertionSort = new InsertionSort();
MergeSort mergeSort = new MergeSort();
QuickSort quickSort = new QuickSort();
RadixSort radixSort = new RadixSort();
SelectionSort selectionSort = new SelectionSort();
int[] nums = getRandomNums();
int[] tmp = new int[NUMS_LENGTH];
System.arraycopy(nums, 0, tmp, 0, NUMS_LENGTH);
// System.out.println("待排序数组:" + Arrays.toString(nums));
long startTime = System.currentTimeMillis();
bubbleSort.bubbleSort(nums);
System.out.println("冒泡排序 " + NUMS_LENGTH + " 个元素用时:" + (System.currentTimeMillis() - startTime) + "毫秒");
// System.out.println("已排序数组:" + Arrays.toString(nums));
nums = tmp;
startTime = System.currentTimeMillis();
insertionSort.insertionSort(nums);
System.out.println("插入排序 " + NUMS_LENGTH + " 个元素用时:" + (System.currentTimeMillis() - startTime) + "毫秒");
// System.out.println("已排序数组:" + Arrays.toString(nums));
nums = tmp;
startTime = System.currentTimeMillis();
selectionSort.selectionSort(nums);
System.out.println("选择排序 " + NUMS_LENGTH + " 个元素用时:" + (System.currentTimeMillis() - startTime) + "毫秒");
// System.out.println("已排序数组:" + Arrays.toString(nums));
nums = tmp;
startTime = System.currentTimeMillis();
quickSort.quickSort(nums, 0, NUMS_LENGTH - 1);
System.out.println("快速排序 " + NUMS_LENGTH + " 个元素用时:" + (System.currentTimeMillis() - startTime) + "毫秒");
// System.out.println("已排序数组:" + Arrays.toString(nums));
nums = tmp;
startTime = System.currentTimeMillis();
mergeSort.mergeSort(nums, 0, NUMS_LENGTH - 1);
System.out.println("归并排序 " + NUMS_LENGTH + " 个元素用时:" + (System.currentTimeMillis() - startTime) + "毫秒");
// System.out.println("已排序数组:" + Arrays.toString(nums));
nums = tmp;
startTime = System.currentTimeMillis();
heapSort.heapSort(nums);
System.out.println("堆排序 " + NUMS_LENGTH + " 个元素用时:" + (System.currentTimeMillis() - startTime) + "毫秒");
// System.out.println("已排序数组:" + Arrays.toString(nums));
nums = tmp;
startTime = System.currentTimeMillis();
radixSort.radixSort(nums);
System.out.println("基数排序 " + NUMS_LENGTH + " 个元素用时:" + (System.currentTimeMillis() - startTime) + "毫秒");
// System.out.println("已排序数组:" + Arrays.toString(nums));
nums = tmp;
startTime = System.currentTimeMillis();
bucketSort.bucketSort(nums);
System.out.println("桶排序 " + NUMS_LENGTH + " 个元素用时:" + (System.currentTimeMillis() - startTime) + "毫秒");
// System.out.println("已排序数组:" + Arrays.toString(nums));
}
}
排列 10000 个元素的耗时对比
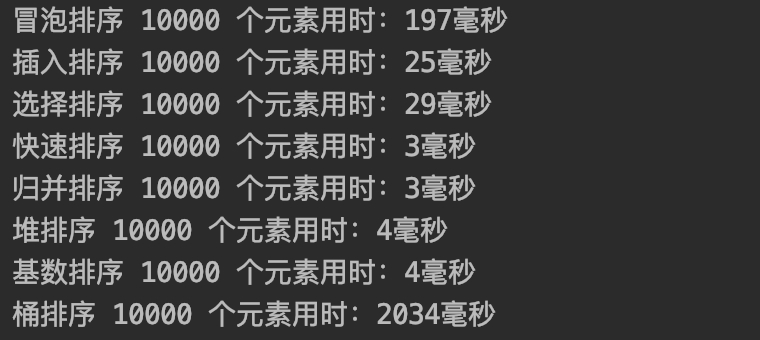
排列 100000 个元素的耗时对比

排列 300000 个元素的耗时对比
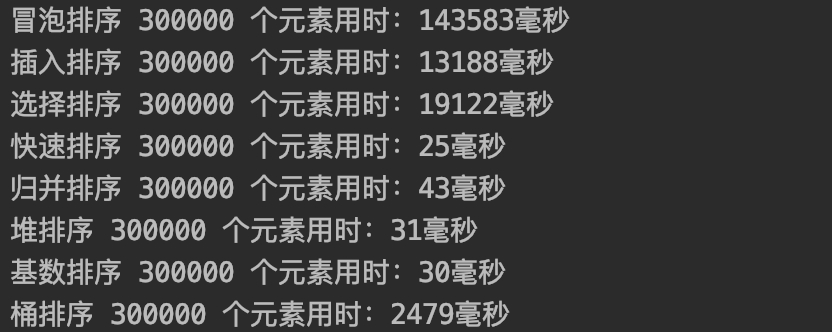
最终,快速排序实至名归,拿下所有测试的 MVP!